How to normalize a mantissa

A floating point number is normalized when we force the integer part of its mantissa to be exactly 1 and allow its fraction part to be whatever we like.

For example, if we were to take the number 13.25, which is 1101.01 in binary, 1101 would be the integer part and 01 would be the fraction part.

I could represent 13.25 as 1101.01*(2^0), but this isn’t normalized because the integer part is not 1. However, we are allowed to shift the mantissa to the right one digit if we increase the exponent by 1:

  1101.01*(2^0)
= 110.101*(2^1)
= 11.0101*(2^2)
= 1.10101*(2^3)

This representation 1.10101*(2^3) is the normalized form of 13.25.

That said, we know that normalized floating point numbers will always come in the form 1.fffffff * (2^exp)

For efficiency’s sake, we don’t bother storing the 1 integer part in the binary representation itself, we just pretend it’s there. So if we were to give your custom-made float type 5 bits for the mantissa, we would know the bits 10100 would actually stand for 1.10100.

Here is an example with the standard 23-bit mantissa:

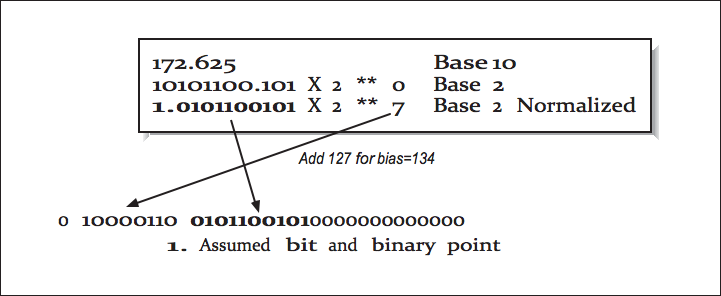
As for the exponent bias, let’s take a look at the standard 32-bit float format, which is broken into 3 parts: 1 sign bit, 8 exponent bits, and 23 mantissa bits:

s eeeeeeee mmmmmmmmmmmmmmmmmmmmmmm

The exponents 00000000 and 11111111 have special purposes (like representing Inf and NaN), so with 8 exponent bits, we could represent 254 different exponents, say 2^1 to 2^254, for example. But what if we want to represent 2^-3? How do we get negative exponents?

The format fixes this problem by automatically subtracting 127 from the exponent. Therefore:

  • 0000 0001 would be 1 -127 = -126
  • 0010 1101 would be 45 -127 = -82
  • 0111 1111 would be 127-127 = 0
  • 1001 0010 would be 136-127 = 9

This changes the exponent range from 2^1 ... 2^254 to 2^-126 ... 2^+127 so we can represent negative exponents.

Related Posts:

  1. Correct format specifier for double in printf
  2. What is the difference between float and double?
  3. Floating point exception (core dumped)
  4. Scanf/Printf double variable C
  5. C: printf a float value
  6. waitpid, wnohang, wuntraced. How do I use these
  7. How to initialize array to 0 in C?
  8. Sign extend a nine-bit number in C
  9. Warning: assignment from incompatible pointer type
  10. C: error: expected ‘)’ before ‘;’ token
  11. make: Nothing to be done for `all’
  12. Data argument not used by format strings in C
  13. execv vs execvp, why just one of them require the exact file’s path?
  14. difference between and
  15. expected expression before ‘{‘ token
  16. Setting std=c99 flag in GCC
  17. C Vector/ArrayList/LinkedList
  18. Warning/error “function declaration isn’t a prototype”
  19. Returning an array using C
  20. warning: initializer element is not computable at load time
  21. Difference between decimal, float and double in .NET?
  22. C convert floating point to int
  23. error: ‘for’ loop initial declarations are only allowed in C99 mode [duplicate]
  24. c – warning: implicit declaration of function ‘printf’
  25. Flushing buffers in C
  26. What are 0x01 and 0x80 representative of in C bitwise operations?
  27. How to make parent wait for all child processes to finish?
  28. Undefined Reference issues using Semaphores
  29. What is time(NULL) in C?
  30. Use of cudamalloc(). Why the double pointer?
  31. Float and double datatype in Java
  32. Portable way to check if directory exists [Windows/Linux, C]
  33. OpenGL — GL_LINE_LOOP —
  34. How to use EOF to run through a text file in C?
  35. Incorrect checksum for freed object on malloc
  36. Valgrind complains with “Invalid write of size 8”
  37. Expression must be a pointer to a complete object type using simple pointer arithmetic
  38. Simple way to check if a string contains another string in C?
  39. What does “request for member ‘*******’ in something not a structure or union” mean?
  40. Segmentation fault (core dumped) due to fgets – I think
  41. C subscripted value is neither array nor pointer nor vector when assigning an array element value
  42. What does “request for member ‘*******’ in something not a structure or union” mean?
  43. Unknown ending signal when using debugger gdb
  44. Valgrind: invalid read of size 4 -> sigsegv, works fine without valgrind and in visual studio
  45. error: too few arguments to function `printDay’ (C language)
  46. How to convert integer to char in C?
  47. Is there a good Valgrind substitute for Windows?
  48. Difference between sizeof(char) and sizeof(char *)
  49. Difference between “move” and “li” in MIPS assembly language
  50. How to empty a char array?
  51. What is the difference between array and enum in C ?
  52. Undefined reference to main – collect2: ld returned 1 exit status
  53. How can one see content of stack with GDB?
  54. What does the term “empty loop” refer to exactly in C and C++?
  55. Is there a way to have printf() properly print out an array (of floats, say)?
  56. What integer hash function are good that accepts an integer hash key?
  57. Proper way to empty a C-String
  58. malloc(): memory corruption
  59. How do you allow spaces to be entered using scanf?
  60. X86 assembly – Handling the IDIV instruction
  61. What do F and D mean at the end of numeric literals?
  62. Pause screen at program completion in C
  63. Where is the header file on Linux? Why can’t I find ?
  64. Difference between fgets and fscanf?
  65. What is the difference between %g and %f in C?
  66. Why is the sizeof(int) == sizeof(long)?
  67. Can’t understand the working of getint() in C as per K&R
  68. Structure padding and packing
  69. Lua – Number to string behaviour
  70. How to allocate array of pointers for strings by malloc in C?
  71. Reading in double values with scanf in c
  72. Realloc Invalid Pointer in C
  73. What tools are there for functional programming in C?
  74. typedef fixed length array
  75. “-bash: gcc: command not found” using cygwin when compiling c?
  76. How to format strings using printf() to get equal length in the output
  77. In C, what exactly happens when you pass a NULL pointer to strcmp()?
  78. In C, what exactly happens when you pass a NULL pointer to strcmp()?
  79. lseek/write suddenly returns -1 with errno = 9 (Bad file descriptor)
  80. What are the differences between if, else, and else if? 
  81. strtok segmentation fault
  82. Invalid write of size 1
  83. How to solve static declaration follows non-static declaration in GCC C code?
  84. realloc(): invalid next size when reallocating to make space for strcat on char *
  85. Constructor for structs in C
  86. C Error: declaration shadows a local variable — Won’t let me repeatedly replace the value of my float variable
  87. MIPS to C Translation
  88. Pointer to 2D arrays in C
  89. Pointer to a string in C?
  90. gdb: No symbol “i” in current context
  91. Cross Platform C library for GUI Apps?
  92. Implicit function declarations in C
  93. Pre increment vs Post increment in array
  94. Convert long long to string in C?
  95. Using pointer to char array, values in that array can be accessed?
  96. How can I create a dynamically sized array of structs?
  97. how to stop a loop arduino
  98. Level vs Edge Trigger Network Event Mechanisms
  99. How to use shared memory with Linux in C
  100. When is it ok to use a global variable in C?

Leave a Comment